
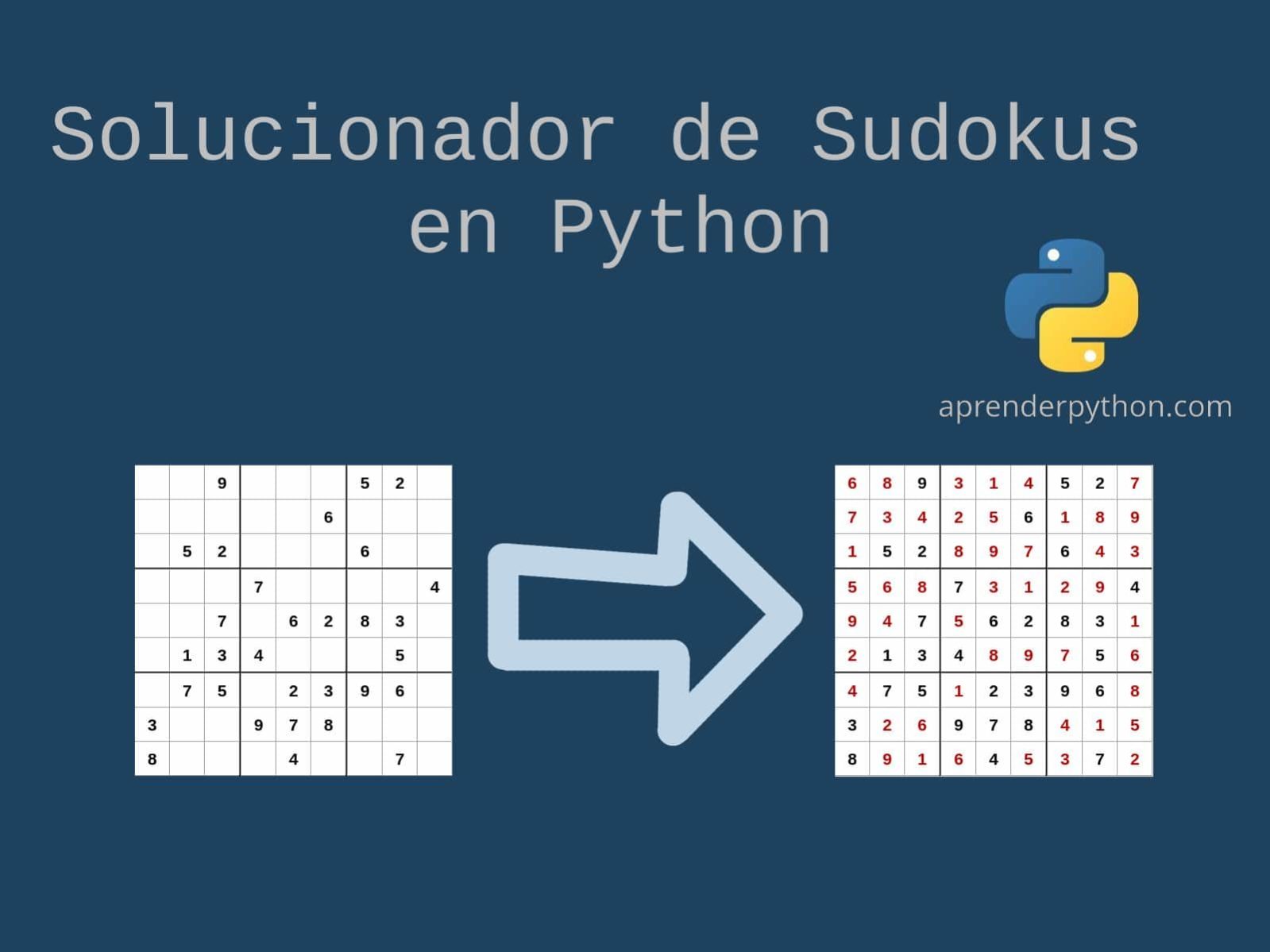
You might try to fill in obvious squares that only have one option and then fill in other squares that have fewer options, while this algorithm systematically goes down the rows and columns to examine the possibilities for each square.Let’s build a sudoku solver in Python today! Sudoku Puzzle is a very popular puzzle that appears in the daily newspaper that attracts the attention of a lot of people. The algorithm used in this post doesn't really mimic how humans solve the puzzles either. The main downside of using backtracking is that it can be very slow, which you can likely imagine just thinking about iterating through each number choice 1-9 for each of the 81 squares in the puzzle, and then adding in the backtracking. In this post we generated and solved Sudoku puzzles using a backtracking algorithm. When multiple solutions are counted, the last number removed is put back into the puzzle and then it continues on selecting non-empty squares to try to remove.Īfter completing the rounds, we are left with the puzzle from above.
#SUDOKU SOLVER PYTHON CODE#
In the code the rounds variable starts at 3 and is decremented each time we find multiple solutions to a puzzle, so that it won't just stop after the first time it encounters a puzzle with multiple solutions. I've made a copy of the grid for each iteration of removing numbers and testing to see if there is a unique solution. In this code, numbers are removed one at a time and each time the puzzle is tested to see how many solutions there are. A puzzle might not even exist with a certain exact number of clues. You could indicate a certain number of clues you want to leave in the puzzle - but this might take forever to run because it might have to backtrack a lot in order to have exactly the number of clues. There are a few ways you could go about removing the numbers. #if there is more than one solution, put the last removed cell back into the grid #might need to put the square value back if there is more than one solution While rounds > 0 and non_empty_squares_count >= 17: Non_empty_squares_count = len(non_empty_squares) Non_empty_squares = self.get_non_empty_squares(id) """remove numbers from the grid to create the puzzle"""

Remove numbersĪfter generating a complete solution grid, it's time to start removing numbers to create the puzzle. It calls other functions to determine whether or not the current number choice already exists in the same row, column, or box.

The function valid_location checks whether or not a number choice can legally be put in a square.
#SUDOKU SOLVER PYTHON FULL#
If there is a partial solution grid and the algorithm gets through all of the rest of the squares without reaching a full solution, then the function returns False and backtracks by replacing the last square in the partial solution with a 0 and starting over. The function returns True if there are no more empty squares. The number choices 1-9 are shuffled(a random permutation of their order is generated) because otherwise the same solution grid would be generated each time. So we test each number in each square and recursively check the rest of the board until we find a solution, which is why it's a brute force algorithm. If it doesn't lead to a solution, then you unchoose by removing that number from the square and trying the next number choice.Now explore recursively to find out if putting a the chosen number in that square will lead to a valid, unique solution.Choose a number 1-9 that could go in the square, and if it's valid(not already in the same row/column/box), assign it to that square.In this code you can see the choose -> explore -> unchoose pattern as we iterate through the squares in the grid. If self.valid_location(grid,row,col,number): """generates a full solution with backtracking""" Instead of starting all over again each time it realizes that a solution will not be viable, it takes a step back and then continues in a different direction. each number 1-9 can only occur once in a column, row, or 3x3 boxīacktracking is a brute force search algorithm that incrementally builds a solution, and backtracks when it takes a direction in the search path that will not lead to a solution.each square must contain a number from 1-9.Backtracking algorithmīacktracking is a type of depth-first search algorithm that can be used to find some or all solutions to a problem, and is often used for constraint satisfaction problems such as Sudoku or crossword puzzles, or the eight queens puzzle. The code for this post can be found here. There are a few algorithms that can be used to solve Sudoku puzzles, and in this post I'm going to use a backtracking algorithm to generate and solve Sudoku puzzles. Check out this article to read more about how puzzles with fewer than 17 clues will have more than one unique solution.


 0 kommentar(er)
0 kommentar(er)
